Scanning tunneling microscopy (STM) is another tool to image surface states in a topological insulator. In the process of STM we tunnel electrons into the surface from a metallic tip. In contrast to ARPES, the electrons are not going into free space, so we don’t have momentum resolution. On the other hand, we do trade momentum resolution for nearly atomic spatial resolution. We know where exactly on the surface the electron came from.
Tunneling into a uniform surface can tell us a little bit about which orbital on an atom, the electrons at a certain energy come from. Otherwise, we’d see a uniform surface, which wouldn’t have much information. We can make things more interesting and, strangely enough, get more information by sprinkling some impurities on the surface. The impurities scatter the surface electrons and produce a standing wave pattern on the surface, which depends on the Fermi surface momenta of the electrons at the particular tunneling energy (Note: in this unit we refer to the equal energy surface in momentum space at the tunneling energy as Fermi surface for convenience). The resulting pattern is referred to QPI. Specifically, Fourier transforming the QPI pattern directly maps out the momentum transfer across the Fermi-surface of the surface state.
Clearly, we can expect to map out some properties of the momentum space scattering on the surface of the topological insulator.
In the simulation below. we see that the Fourier transform shows an interesting pattern:
 (adapted, copyright Hasan lab, Princeton, see license in the beginning of the chapter)
(adapted, copyright Hasan lab, Princeton, see license in the beginning of the chapter)
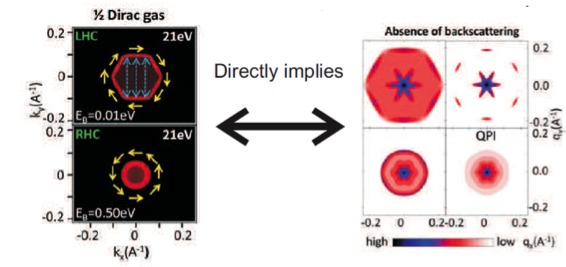
By comparing the QPI patterns showing spin-dependent and spin-independent scattering (respectively on the left and right column on the right side of the arrow), we see that the intensity at momenta connecting opposite points on the Fermi surface is suppressed in the case of spin-independent scattering.
In fact, by comparing the fourier transform of the QPI on the right with the Fermi surface on the left, we begin to see that the absence of back-scattering, which is one of the key properties of the topological insulator surface state plays a key role. As you might remember from the quantum spin hall systems - elastic backscattering of electrons is forbidden between states at \(\bf k\) and \(-\bf k\) because of Kramers’ theorem. Looking at the QPI pattern from spin-independent impurities and comparing it with the Fermi surface confirms this.