In the image below (source: Chambers’s Encyclopedia, 1875, via Wikipedia) you see a very simple periodic time-dependent system, an Archimedes screw pump.

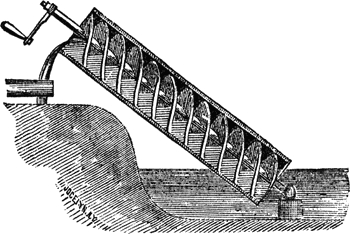
The changes to the system are clearly periodic, and the pump works the same no matter how slowly we use it (that is, change the parameters), so it is an adiabatic tool.

What about a quantum analog of this pump? Turns out it is just as simple as you would think.

Let’s take a one-dimensional region, coupled to two electrodes on both sides, and apply a strong sine-shaped confining potential in this region. As we move the confining potential, we drag the electrons captured in it.

So our system now looks like this:

It is described by the Hamiltonian

\[H(t) = \frac{k^2}{2m} + A [1 - \cos(x/\lambda + 2\pi t/T)].\]

As we discussed, if we change \(t\) very slowly, the solution will not depend on how fast \(t\) varies.

When \(A \gg 1 /m \lambda^2\) the confining potential is strong, and additionally if the chemical potential \(\mu \ll A\), the states bound in the separate minima of the potential have very small overlap.

The potential near the bottom of each minimum is approximately quadratic, so the Hamiltonian is that of a simple Harmonic oscillator. This gives us discrete levels of the electrons with energies \(E_n = (n + \tfrac{1}{2})\omega_c\), with \(\omega_c = \sqrt{A/m\lambda^2}\) the oscillator frequency.

We can quickly check how continuous bands in the wire become discrete evenly spaced bands as we increase \(A\):

So unless \(\mu = E_n\) for some \(n\), each minimum of the potential contains an integer number of electrons \(N\).

Electron wave functions from neighboring potential minima do not overlap, so when we change the potential by one time period, we move exactly \(N\) electrons.